What is Hydraulics?

Table of Contents

• Definition and Origin of the Term Hydraulics
• History of Hydraulic Systems
• How Did Hydraulics Come into Existence?
• Pascal’s Law
• Mathematical Formula of Pascal’s Law
• Applications of Pascal’s Law
• Conclusion

Definition and Origin of the Term Hydraulics

The word hydraulics originates from the Greek term “hydraulikos,” which itself is derived from “hydor,” meaning water, and “aulos,” meaning pipe. Hydraulics is essentially a mechanical operation that functions through the force generated by fluid pressure.

In hydraulic-based systems, force is typically produced by the mechanical motion of pistons moving within hydraulic cylinders filled with liquid or pumped fluid.

Although the term hydraulics includes the word water, in practice, water is not used as a fluid in hydraulic systems due to its corrosive and rust-inducing properties on metal materials. Instead, oil is commonly used as the hydraulic fluid.

History of Hydraulic Systems

In ancient times, hydraulic systems were extensively used in an open-loop format. For instance, the hydraulic system utilized in Shushtar serves as an example of such applications. Below, you can see an image of this hydraulic system in Shushtar.

How Did Hydraulics Come into Existence?

It is difficult to determine precisely who invented hydraulics, when, and how. However, the use of hydraulic-based systems can be traced back to the 1st century AD.

Blaise Pascal, a French physicist, mathematician, inventor, and philosopher who lived between 1623 and 1662, made significant contributions to the fields of hydrostatics and hydrodynamics. He invented the first hydraulic press, which utilized hydraulic pressure to amplify forces. Additionally, he formulated Pascal’s Law, also known as the Principle of Hydrostatics.

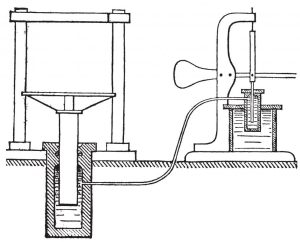
Pascal’s Law

Pascal’s Law

Pascal’s Law (or Pascal’s Principle) is a fundamental principle in fluid mechanics. It states that in a state of equilibrium, an incompressible fluid enclosed in a confined space transmits the pressure applied to it equally and undiminished to all other points within the fluid.

Mathematical Formula of Pascal’s Law:

P=FAP = \frac{F}{A}

Where:

• P: Pressure in pascals (Pa)
• F: Force applied to the surface in newtons (N)
• A: Cross-sectional area in square meters (m²)

Applications of Pascal’s Law:

To better understand the application of Pascal’s principle in hydraulic systems, consider the diagram below, which illustrates a closed system. Two pistons with different cross-sectional areas but positioned at the same height relative to each other (equilibrium state) are shown.

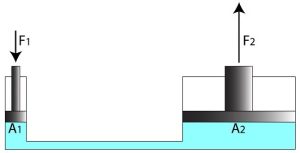
In the diagram above,

The cross-sectional area of the left piston is represented as A1, and the force applied to it as F1. The cross-sectional area of the right piston is represented as A2, and the force applied to it as F2. When a force F1 is applied to the left piston, it causes the piston to move downward, which in turn pushes the fluid below it. This results in the fluid transmitting the force F2 to the right piston, causing it to move upward by the same amount as the left piston’s downward movement.

If we consider Pascal’s relationship for each piston side, we have:

F1A1=F2A2\frac{F1}{A1} = \frac{F2}{A2}

Since fluids are incompressible, the pressure exerted on the fluid remains the same throughout the hydraulic system. Therefore, we can equate the two sides of the above relationship:

F2=F1×A2A1F2 = F1 \times \frac{A2}{A1}

Conclusion

As derived from the above formula, by applying a smaller force F1 to the smaller area A1 on the left piston, a larger force F2 can be obtained on the right piston with a larger area A2.

This concept forms the foundation of many existing systems, including:

• Press Brakes
• Hydraulic Presses
• Hydraulic Shears
• Hydraulic Bending Machines
• Automotive Brake Systems
• Hydraulic Jacks00
• Cranes
• Elevators

These systems facilitate tasks such as lifting heavy loads, striking metal, or compressing objects.

Below, you can watch a video demonstrating how a hydraulic system works in a hydraulic press and a car braking system.